圧倒的であっという間の3時間!
インターステラーを見てきました。
久しぶりに、誰かとあーだこーだと言いたいくらい面白い映画だったのでこちらに感想を書きます。
まずはオフィシャルサイト貼っておきます。
予告編などの映像ががたくさん見られるので、まだの方はぜひ見て下さい。
普段あまり映画を見に行かない私が映画館に行くくらいなので、映画自体は結構話題になっているのかなと思います。
現に私も、ネット上で「スゴイSF映画!」という感想を見て、SFなら見ようかなと思った次第です。
実際に見て、久しぶりにスゴイなこれ!と思ったので、ネタバレ(下の方)含めて書きます。
ただ、多くの人に見て頂きたいと思ったので、最初はあらすじや知っておくと楽しめる予備知識を書いておきます。
下に行くほどネタバレしていきますので、知りたくないという方は映画を見てから、ぜひまたこちらに来てください。
あらすじ
近未来、地球規模の食糧難と環境変化によって人類の滅亡のカウントダウンが進んでいた。そんな状況で、あるミッションの遂行者に元エンジニアの男が大抜てきされる。そのミッションとは、宇宙で新たに発見された未開地へ旅立つというものだった。地球に残さねばならない家族と人類滅亡の回避、二つの間で葛藤する男。悩み抜いた果てに、彼は家族に帰還を約束し、前人未到の新天地を目指すことを決意して宇宙船へと乗り込む。
ストーリー自体はこのあらすじの通りなのですが、これだと映画の凄さの5%くらいしか伝えてないと思います。
あらすじだけを見ると、人類滅亡と家族というハリウッドに良くありがちなテーマだな、と思ってしまうかも知れません。
確かにストーリーだけを追えば、このあらすじで間違いありません。
さすがシネマトゥデイという感じです。
しかし、この映画の凄さはこのあらすじでは伝わらないのです。
ここから先、軽くネタバレします。
全くまっさらな状態で見たい方は、ここから先見ないで下さい。
見てしまうと映画を見る視点が全く変わってしまいます。
出来ればまっさらな状態で見て、もう一度こちらに来てください。
知っておくと楽しめるSFの知識をこの下に書いていますので、疑問も色々解決するかも知れません。
純粋な親子愛を描いたストーリーに集中したければ、ここからは映画を見た後に見てください。
SFが好きだという方は、おそらくSF目線でしか見られないと思うので、復習がてらにどうぞ。
知っておくと楽しめるSF知識
インターステラーの何がスゴイって、これまでのSF映画には無い描写です。
ゼログラビティにも映像美はありました。
しかし、それ以上にインターステラーは映像がスゴイです。
さらにSFファン以外を置き去りにする用語がバンバン出ます。
現に私と一緒に見た妻は、全くわからなかった、と言っていました(それでもストーリーは楽しめた、とのこと)
ということで、ここからは知っておくとさらに楽しめる予備知識を書いていきます。
二進法とモールス信号(符号)
二進法
二進法は、よくコンピューターとかプログラム界隈で出てきます。
中学数学でも習っているはずですが、普段は中々目にしませんので簡単に解説。
通常私達が使っているのは十進法です。0,1,2,3,とカウントしていくと、9の次は、【10】になり、一桁では表せません。
つまり次の桁に進む、ということです。
二進数はその名の通り「2」で進みますので、0,1とカウントして次は【10】です。
見た目は十進法の【10】と同じですが、全く違います。
二進法の【10】は十進法にすると【2】です。
十進法の【10】は「じゅう」と読みますが、二進法の【10】は「イチゼロ」と読みます。
では二進法で【3】はどう表すか?答えは【11】です。
ジュウイチではなく、「イチイチ」です。
では、二進法で【5】はどうしましょう。
0,1ときて、次は【10】でこれが十進法の2です。
【10】、【11】←これが3ですから、4にするためには桁を増やさなければなりません。
ということで、【100】となり、これが十進法の4になります。
となると、5にするには【101】とすればいいわけです。
ちなみに6は【110】、7は【111】、8は【1000】です。
簡単にまとめます。
0→0
1→1
2→10
3→11
4→100
5→101
6→110
7→111
8→1000
9→1001
10→1010
100→1100100
1000→111110100
と、こんな感じです。
モールス信号(符号)
モールス信号(符号)は戦争映画などで暗号に使われる「トン・ツー・トン・ツー」というやつです。
懐中電灯などの光でも送ることが出来ます。
長音と短音を組み合わせればいいだけなので、長く照らす⇔短く照らすを組み合わせれば同じことです。
ここで二進法とモールス信号(符号)の関係性なのですが、例えば1を長音符、0を短音符とすると、二進法でモールス信号を表現したり出来ます。
モールス信号(符号)には細かい決まりが色々とあるのですが、少し端折って1を長音符、0を短音符として【blog】を変換してみます。
【blog】モールス信号(符号)にすると→ 【-・・・ ・-・・ --- --・】
ではさらに長音符を1にして、短音符を0にしてみます→【1000 0100 111 110】
そうすると、これを二進法→十進法に変換したり出来そうですね。
【1000】は8、【0100】は4、【111】7、【110】は6 です。
例えば、私の8476へようこそ!(十進法→二進法→モールス符号変換でよろしく!)なんて書いておくことも出来ますね。
本当は、もう少し細かい決まりがあるので、興味があればWikipedia(モールス符号)をどうぞ。
二進法とモールス信号(符号)をまとめ
さて少し難しいかも知れないのでまとめると、モールス信号(符号)、もしくは二進法を駆使することで、トン・ツー、あるいは1、0だけで文章を作ることが出来るということです。
0を空白にする、というルールを決めれば「 1 1 1」というようなことも可能だということです。
これを知っていると、インターステラーの中でどうしてそれで伝わるの?という謎がわかります。
銀河系
私達の住んでいる地球は、銀河の中の太陽系に属しています。
同じ太陽系に属しているのは、水星、金星、火星、木星、土星などがあり、これらの星が太陽の周りを回っています。
太陽の様に自ら光を放つ星を恒星と呼び、地球は太陽の光を浴びて輝いているに過ぎません。
惑星と似た言葉で、衛星というものがあります。
ざっくり言えば惑星の周りを回っている星のことで、地球の衛星は月です。
月は地球の周りを回っているだけですので、もしも地球がどこかに飛ばされた場合には、月もついてきます。
他に有名な衛星としては、木星の衛星であるエウロパ、ガニメデなどがあります。
さて、あまり細かい話は映画の上では重要ではなくて、銀河が何かということが重要です。
まず、惑星がいくつか集まって太陽系のような系列を作ったり、星団を作ったりします。

太陽系
そしてこの様な太陽系は、私達の太陽系だけではなく無数にあります。
単純に星が集まって出来た星団と呼ばれるものもあります。
これらの星団や恒星などが集まって出来るのが銀河です。
銀河一つに1000万~100兆の星が集まっています。

渦巻銀河(NGC_4414)
上の画像は渦巻銀河と呼ばれる銀河です(ここに数千万~数兆の星が集まっている。)
銀河にも色々と形がありまが、ここでは割愛。
人が集まって村に、村が集まって町に、町が集まって市→都道府県→国になる。
という感じです。
銀河団
つまり銀河にはたくさんの星があって、銀河という国のような物を形成しているということです。
私達の住む地球がある銀河だけでも、太陽と同じような星が2000億個あると言われています。
地球にたくさんの国があるように、銀河も私達の銀河だけではなく他の銀河も存在します。

かみのけ座銀河団
上の画像で光って見えるものは星ではなく、一つ一つが銀河です。
銀河が集まったものを銀河団と呼びます。
こうして銀河が無数にあって、銀河団を形成しているのはわかっているのですが、私達の科学力では太陽系の外に出るのがやっとです。
とはいえ、動物はまだ出ることが出来ていません。
36年前に打ち上げられたボイジャー1号がやっと外に出ただけです。
ところで、人間は月まで行ったことがあります。
月までの距離は約38万kmで、時速300kmで進むと約53日かかります。
では、銀河の端から端までの大きさはどのくらいでしょうか?
正解は10万光年。
この1光年という単位は、光が一年間に進む距離のことです。
地球から月までの距離は38万kmですが、これを光年に直すと約0.00000004光年です。
光年(こうねん)
1光年は、光が一年間に進む距離を表します。
宇宙では距離がとにかく大きくなるため、光年という単位をよく使います。
1光年は約9.5兆kmで、数字で書くと9,500,000,000,000kmです。
光が進む距離と言ってもピンと来ないかも知れませんが、光も車や電車の様に実際は進んでいます。
ただあまりにもスピードが速いため、スイッチを入れた瞬間に光が見える、というだけのことです。
もしも1光年向こうに懐中電灯を照らそうと思ったら、スイッチを入れた1年後にそこが照らされる、という感じです。
光の速さがどのくらいか、いくつか示してみます。
・地球一周→4万km(40,000km)
・地球から月までの距離→38万km(380,000km)
・光が一秒間に進む距離→30万km(300,000km)
・光は一秒間で地球を7周半出来る
・時速に直すと1億800万km(108,000,000km)
・新幹線の最高速を300kmとすると、光はその36万倍のスピード。
・新幹線で月まで行くと53日かかるが、光なら1秒半で行ける。
どうでしょうか?光の速さがわかってもらえたと思います。
さて、私達の住む地球が太陽系、そして銀河の中にある、という説明を上記でしましたが、その銀河の大きさは10万光年。
つまり、光の速さで10万年かかるということです。
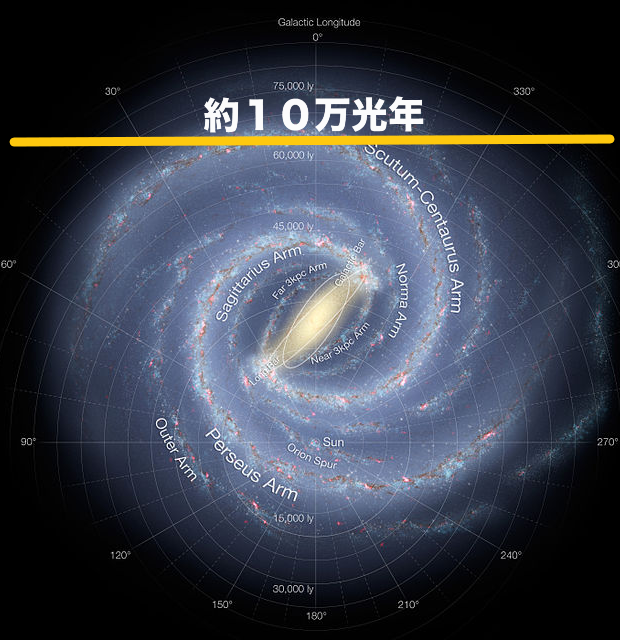
天の川銀河イメージ図
仮に私達の地球が、銀河の中心にあるとしましょう。
それでも端に行くまでに光の速さで5万年です。
キロメートルにして、4,730,642,000,000,000,000,000,000km(4予730垓km)
時速300kmの新幹線に乗って行ったとして、1,800,092,085,000,000,000年(180京年)
どうあがいても銀河を脱出するのは無理です。
ちなみにすぐ隣りの銀河は、太陽系から2万5千年のおおいぬ座銀河です。
新幹線で90京年で行ける計算ですが、一人の人生を80年とすると11,250,000,000,000,000世代必要です。
ワームホール
隣の銀河まで行くのはまず無理、ということがわかりましたが、これを解決する方法があります。
ワームホールです。
ワームホールが通過可能な構造であれば、そこを通ると光よりも速く時空を移動できることになる。ワームホールという名前は、リンゴの虫喰い穴に由来する。リンゴの表面のある一点から裏側に行くには円周の半分を移動する必要があるが、虫が中を掘り進むと短い距離の移動で済む、というものである。
Wikipediaより引用
ざっくり言うとワープゾーンです。
この穴を通れば時空を歪めてワープ出来る、ということです。
ワームホールを説明する時によく使われるのが下のやり方です。
何でもいいので、紙の対角線上に線を引きます。
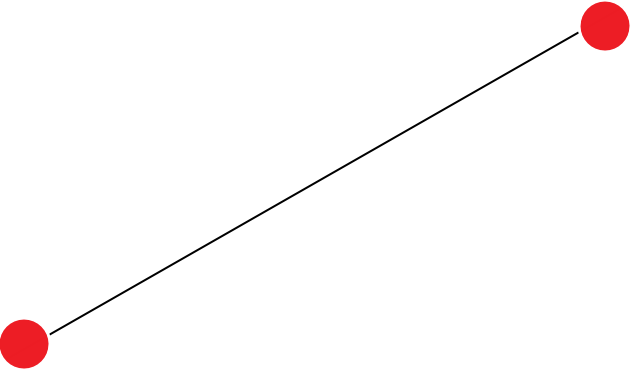
赤い点はそれぞれ銀河とする
赤い点(銀河)同士を移動するには、まっすぐに線を引くのが最短距離です。
紙を宇宙とすると、線は宇宙船での航路となります。
ではこの二つをもっと早く移動するにはどうすれば良いかというと、以下の図のようにすればいいわけです。
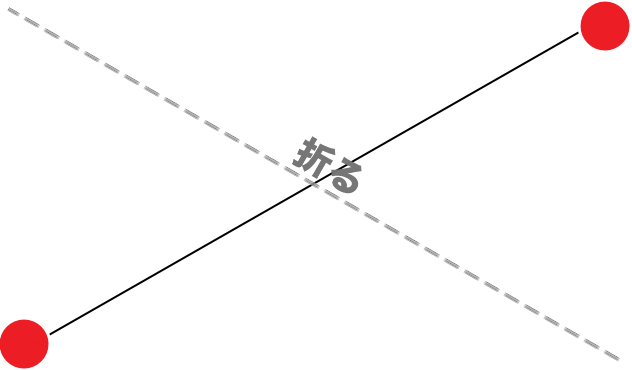
ワームホール-2
宇宙という空間そのものを歪めてあげれば、二つの銀河を簡単に行き来出来ます。
これがワームホールの考え方です。
もちろん、現代科学では作り出すことは出来ません。
次元(じげん)
ルパ~ンの次元ではありません。
四次元ポケットでお馴染みの次元です。
http://ja.wikipedia.org/wiki/次元のページにある図がわかりやすいので、こちらを掲載します。
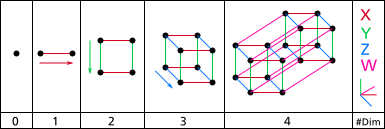
次元の概念図
私達の住む世界は立体世界なので三次元と言っていいでしょう。
細かい話は色々ありますがここでは省略。
アニメキャラは平面上(紙)に存在するので二次元キャラと呼ばれたりします。
三次元世界に住む私達は、二次元世界を折りたたんだり曲げたり出来ます。
しかし空間を折りたたむことは出来ません。
もし空間を折りたたむことが出来るとすれば、それはワームホールを作るということになります。
これと同じ様に、四次元世界に住むものは三次元世界を自由に扱うことが出来るのです。
つまり、ワームホールを作り出すことが出来るのは、四次元世界の人々ということになります。
では、三次元に何をプラスすれば四次元になるのか。
SF的に答えると「時間」です。
四次元世界は時間を自由に行き来することが出来ると考えれば良いと思います。
ドラえもんは四次元空間をタイムマシンを使って自由に行き来します。
また、四次元ポケットはあの小さな中に何でも詰め込むことが出来ます。
どうしてそんなことが出来るのか?空間を歪めることが出来るからです。
しかし、四次元でもまだ時間そのものをコントロールすることは出来ません。
私達が空間そのものをコントロール出来ないのと一緒です。
時間そのものをコントロールするためには、さらに上の次元に行かねばなりません。
これが五次元世界となるわけです。
では、五次元世界とは何なのか?これは正直わかりません。
基本的には、自分の次元より上の次元世界を見ることは出来ないからです。
三次元世界は四次元世界を見ることは出来ないですし、二次元世界の住人は、三次元世界を見ることは出来ません。
紙の世界に描かれたキャラは、立体的な私たちの世界を認識することは出来ないのです。
だから、私達は五次元世界がどういうものかわからないのです。
ですが、空間をコントロールするのが四次元ですから、時間と空間の両方をコントロールすることが出来る世界は五次元と言えます。
私達が平面の紙を折りたたむことが出来るのと同じです。
紙を折りたたむのにわざわざ小難しいことは考えないですよね?
これと同じくらいの感覚で空間や時間を簡単にいじることが出来るのが五次元世界です。
時間をたたんだり、空間をくしゃくしゃにすることも出来る、ということです。
あれ?いやいや、私達も時間の概念は持ってるから四次元では?と思った方は、http://ja.wikipedia.org/wiki/次元のページを見て悶々とすると良いかと。
今回はあくまでインターステラーを見るための知識、ということで細かい話は省略します。
重力
インターステラーでは重力は重要なワードです。
単純に物が下に落ちるのを重力というわけではありません。
重力の話をするためにはまず、「引力」に触れなければいけません。
リンゴが木から落ちるのを見たニュートンが発見したとされる万有引力の法則(今では作り話となっていますが)は、全ての物はお互いに引き付け合う、という力です。
そしてこの引き付け合う力は質量が大きいほど大きくなるのです。
ざっくり言えば、質量とは重さです。
重たいということは、質量が大きいから引きつけ合っているということになるのです。
では私達は、一体何に引きつけられているから重さを感じるのでしょうか?
それは、地球です。
地球はものすごく質量が大きいです。
この地球に地球上のものは全て引きつけられているのです。
これが万有引力の法則です。
地球に引きつけられている、というイメージはしづらいと思いますが、地球は自転しています。
これは、遊園地のコーヒーカップに乗っているようなものですから、遠心力が働きます。
何かに捕まらなければ飛んで行ってしまうはずですが、飛んでいかないのは地球に引きつけられているからです。
そして、この遠心力と引力のせめぎ合った部分を地球上の重力と呼びます。
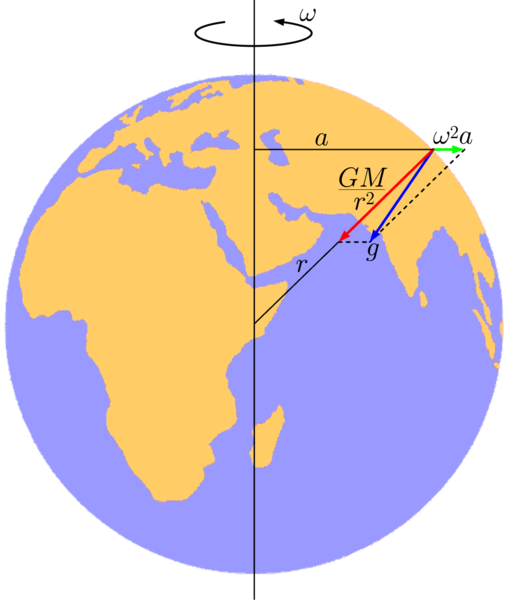
地球の重力イメージ
宇宙では星同士も引き付け合っています。
地球が太陽の周りを回っているのは太陽の引力に引き付けられているから。
もしも引力が無ければ、地球は太陽の周りを回らずどこかに吹っ飛んでいきます。
地球が吹っ飛んでいく力を、太陽が引きつけることでうまくバランスを取っているのです。
重力は地球上の全てのものに作用していますので、これをコントロールすることが出来ると科学は飛躍的に進歩すると言われています。
しかし、現代物理学ではまだ不可能とされています。
ブラックホール
ブラックホールの事は詳しくはわからないけれど、とにかく何でも吸い込むやつでしょ?とご存知の方も多いと思います。
インターステラーではブラックホールがかなり重要な役割を果たしてますので、知っておくとかなり楽しめます。
ブラックホールとはものすごい質量を持った天体のことです。
万有引力の法則で、質量が大きければ大きいほど引き付け合うと説明をしましたが、ブラックホールは最強の質量を持っていると思って下さい。
つまり、なんでも引きつけてしまいます。
ブラックホールというと黒い穴で、そこに吸い込まれるとイメージするかも知れませんが実際には穴ではありません。
全ての物を引き付けているということは、光をも引きつけているということです。
光が引きつけられるということは、ここに懐中電灯を照らしても反射した光が出て来られない為何も見えないということです。
ではどうしてそこにブラックホールがあると言えるのか?というと、周りの光が重力により捻じ曲げられおかしな空間となっているからです。
wwikipediaに良い画像がありましたので掲載します。

天の川を背景としてブラックホールがあったら、というイメージ図
イメージとしてはこんな感じです。
とにかく何でも引き寄せると思って下さい。
そしてその力は、中心に行けば行くほど強くなります。
中心部に近づいていき、ある一定の半径を超えると光すら脱出することが出来なくなります。
逆を言えばその半径を超えるまでは、光であればなんとか脱出出来るということです。
もしも光を自在に捻じ曲げる事ができれば、ブラックホールにかなり近づいて観測することが出来ます。
そして、光すら脱出出来なくなる半径のポイントを【シュヴァルツシルト半径】もしくは【事象の地平面】と呼びます。
ちなみに、この光が脱出できなくなるポイントを人工的にでも作り出すことが出来れば、ブラックホールは作ることが出来ます。
地球をぎゅーっと小さく丸めて、およそ直径9mmほどにすることが出来ればブラックホールになります。
それだけ密度を高くすると質量がものすごく大きくなり、光が脱出できないほどの重力を持つからです。
事象の地平面(シュヴァルツシルト半径)
ブラックホールを語る上で切っても切れないのが事象の地平面です。
簡単に言えば、「二度と引き返すことが出来ない領域」です。
ブラックホール中心から一定の距離にこの事象の地平面が存在します。
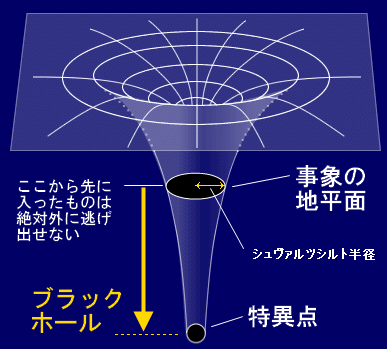
ブラックホール図解 シュタインズゲートまとめより
この領域を超えてしまうと光すら脱出出来なくなります。
これは、ブラックホールの巨大な重力に光も引き寄せられてしまうからです。
ロケットなどは事象の地平面よりもはるか手前で脱出不可能になります。
事象の地平面という名前は、【事象】つまり何かが起きていることが観測できる最終地点、という意味を持っています。
光が脱出できないので、何が起こっているのか見ることが出来ないのです。
ブラックホール中心部では何が起きているのか、実は未だに謎なのです。
数学的な計算をして、多分こんなことが起きているだろうという想像は出来ますが、実際に見ることは出来ません。
特異点
事象の地平面と同様に、ブラックホールと切っても切れないのが特異点です。
重力の特異点、と呼ばれたりもします。
ブラックホールは光すら脱出できない為、見ることが出来ません。
要するに、事象の地平面より内側については全くわからないのです。
しかしそれじゃあ面白くない、ということで数学や物理計算で内部がどうなっているのかを解明しようとしています。
で、色々と計算はしているのですが、どうやって計算しても通常の物理法則では説明できない事が起きてしまいます。
この、物理的法則では説明できない事を特異点と呼びます。
特異点という呼び方自体はブラックホール以外でも使われます。
ブラックホールでは【重力の特異点】が有名です。
ここまで説明しているように、ブラックホールはとにかく重力が大きく、光すら脱出できません。
では、その重力がどのくらい大きいのか?
これを計算して出そうとすると、なんと無限大になってしまうのです。
無限、というのはありえないのです。
なぜなら、無限の重力だったらこの世の全ての物を引き付けているはずです。
でも実際にはそんなことはありません。
ところが、計算式も間違ってないのです。
どうやって計算しても無限大になってしまうポイントがあるのです。
これが特異点です。
要するに、私達の知っている物理法則や知識では解決出来ないということです。
他の計算方法を編み出さない限り、特異点はどうしても発生してしまいます。
ブラックホールはまだまだ未知の物なのです。
シュヴァルツシルトブラックホールとカーブラックホール
インターステラーで登場するブラックホールはカー・ブラックホールです。
突き詰めるとものすごく難しくなるので、簡単に言うと自転しているかしていないかの違いです。
カー・ブラックホールは自転するブラックホールのことで、一般的にイメージされるブラックホールは、自転しないシュヴァルツシルトブラックホールのことです。
特異点の説明をしましたが、シュヴァルツシルトブラックホールでは特異点は中心部に存在します。
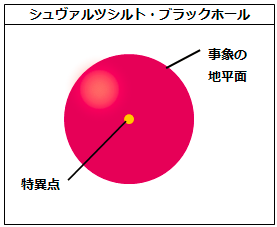
シュヴァルツシルトブラックホール(シュタインズゲートまとめより)
ところが、カーブラックホールでは特異点はリング上に存在します。
このリング上の特異点の中心部を通過することが出来れば、タイムトラベルが可能になるのでは?
というのがSF的な観点です。
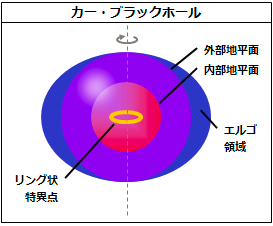
カーブラックホール(シュタインズゲートまとめより)
実際には、特異点に近づくほどの重力の中では、全てがバラバラに引き裂かれてしまうので、タイムトラベル出来たとしてもそこに存在出来ているのかはわかりません。
相対性理論
宇宙へ行くと地上よりも時間の進み方が遅い、あるいは光速に近いスピードで移動すると時間が進むのが遅くなる、ということを聞いたことがあるかもしれません。
どうしてそんなことが起こるのか?
そもそも時間とは何か?
ざっくりと言うと、「時間とは光の速度を基準とした時間の流れ」ということになります。
光の速さ、というのは常に一定で変化はありません。
それならば、光の速さを基準に色々とものを考えたら色々解決するのではないか?と考えたのがあのアインシュタインです。
何かの基準があって、それと比べてどうなのか?というのと【相対性】と呼びます。
何の基準も無くて、そのものだけの数字を【絶対性】と言います。
例えばあなたの身長が170cmだとしましょう。
身長が170cmであることは【絶対性】です。
北極に行こうが、南極に行こうが、海に入ろうが、スカイダイビングをしようが、あなたの身長は170cmです。
しかし、この身長が【高い】のか、【低い】のか、それは場所や環境によって変化します。
NBA選手に囲まれたらあなたの身長は【低い】と思われますし、小学生の列に並んだら【高い】と思われるでしょう。
この様に何かと比べることを【相対性】と呼びます。
で、アインシュタインの【相対性理論】とは何かというと、光の速度を基準とした物理の考え方のことなのです。
つまり、全て光の速度が基準。
時間の流れも、光の速度を基準に考えています。
重力と時間の遅れ
重力と時間の遅れについては研究が進んでいるところですが、重力が強いと時間が遅れるということを知っていれば、この映画は楽しめます。
ものすごーくざっくり言うと、光も重力の影響を受けるためものの見え方が変わるということです。
事象の地平面の存在から、重力は光にも影響をあたえることがわかります。
ブラックホールから脱出しようとしている光を捕まえているから、光が見えなくなるわけです。
ということは、事象の地平面付近では光の進むスピードは遅くなっているということです。
事象の地平面を超えたらいきなり重力が発生するわけではなく、徐々に強力になっていき、そのラインを超えると戻れなくなるのですから、光が徐々に遅くなっていき、最終的には脱出出来なくなるということになります。
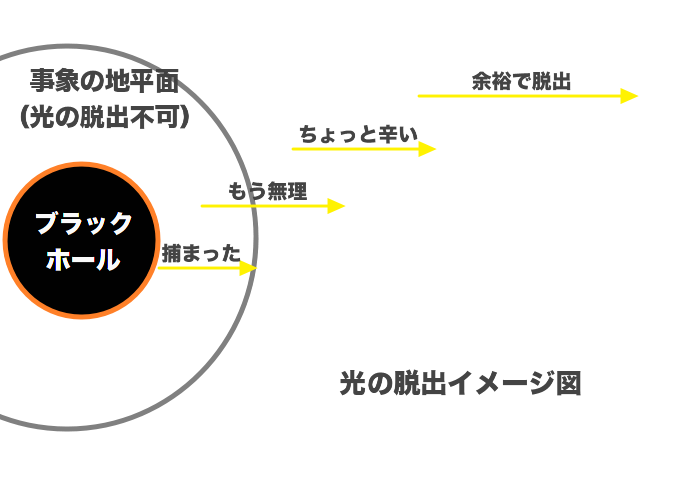
光の脱出イメージ図
しかし光の速度は常に一定である、というのが相対性理論です。
これを基準に時間の流れも考えられているので、光が重力の影響を受けて進み方に変化が出ると時間にも影響があります。
仮にブラックホール付近を光が直進したとすると、以下の図の様になります。
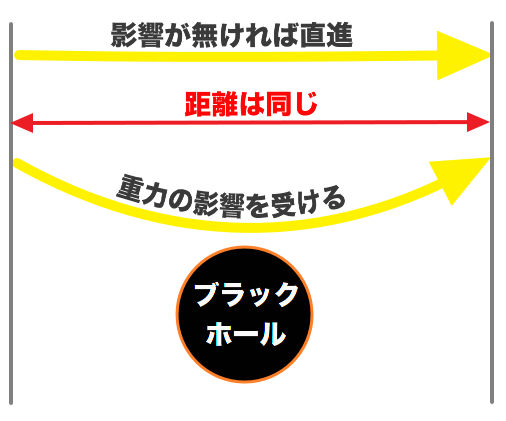
重力による光の進み方
重力によって光が曲がるので、直進した光と同じ距離を進もうとしても、若干距離が伸びるということです。
ところが。
ここからが面白いところなのですが、光の速度は常に一定です。
どのような状況においても、光は一秒間で約30万km進まなくてはなりません。
絶対に、何があろうと光は一秒間で30万km進まなくてはならないのです。
そうしないと、現在存在している時間や、物理の法則が全て狂ってしまうからです。
ということは、上の図の距離が30万kmだったとすると、どちらの光も一秒間で進まなくてはならないのです。
しかし下の光は重力の影響を受けて曲がっていますから、上の光よりも余分に距離を進んでいるわけです。
これはおかしい、ということになります。
光の進むスピードは、一秒間で30万キロ。
これは絶対なのです。何があろうと変わりません。
ということは、図中の下の光は、一秒間で上の光よりも長い距離を進んでいることになります。
同じ一秒間で、下の光は寄り道をしているということです。
これはつまり、上の光と比べて余計なことが出来ているということなります。
もう一度同じ図を用意しました。

重力による光の進み方
下の光のほうが距離が長いですね。
では、この光が電車だったらどうでしょうか?
同じ時間で余計な距離を進むわけですから、寄り道をしている方が弁当一個余計に食べられるかも知れませんし、本も一冊余計に読めるかも知れません。
ではさらに、この光が星だったらどうでしょうか?
ブラックホール付近にある星は重力の影響を強く受けます。
ということは影響を受けていない星や宇宙船に乗っている人よりも、同じ時間で余計な事ができるということです。
上の光がりんごを一つ食べる間に、下の光はりんごを二つ食べることが出来るのです。
つまり、何が言いたいかと言うと、重力の強いところに居ると【通常よりも短い時間で同じことが出来る】ということです。
ということは、重力が強ければ強いほど時間の進み方がゆっくりになる、と言えるわけです。
ただこれはあくまでも外から見た場合です。
重力の影響を受けている人にとってみれば、30分は30分です。
実際にりんごを二つ食べている人からすれば、早く食べているつもりも無いし、時間が遅くなっている感覚もありません。
時間は絶対ではなく、光を基準とした相対的なものなのです。
ブラックホールへの落下
ブラックホールでは重力が無限大になるポイントがあって、これが特異点でした。
ではブラックホールに吸い込まれる人はどうなるのでしょうか?
ブラックホールは内部に近づくほど重力は強くなります。
ということは、実際には落ちるスピードは速くなるハズです。
しかし、ブラックホールの外から見ていると、落ちていく人はどんどんスピードがゆっくりになるように見えます。
見える、ということは光を認識しているということになります(暗闇では何も見えません)
ところがブラックホールでは、光すら進むのが遅くなります。
その為、落ちていく人を見るとゆっくり落ちていくように見えるのです。
光すら脱出出来ない事象の地平面に近づくに連れて、どんどんゆっくりになります。
落ちている本人は凄まじいスピードで落ちていますので、あくまでも外から見た場合です。
そして見ている側からすると、不思議なことが起こります。
事象の地平面で、落ちている人がピタッと止まります(本人はもう真っ逆さまです)
そして、永遠にそこに貼り付いたままです。
実際に落ちる人を見続けた場合真っ赤になりながら落ちていき、事象の地平面に貼り付いた後、光も分散してしまうので、みえなくはなります。
さらに面白い記事がマイナビニュースのもしも科学シリーズにあったので抜粋です。
ブラックホールに人間が落ちたらどうなるか? 足から落ちた場合、ブラックホールの中心に向かってまっすぐ向かっていくことになる。引力は近い物体により強くはたらくので、中心に近い足には大きな引力が、頭には小さな引力がはたらき、加速度の違いが生じる。頭はゆっくりと、足は速く中心へと向かい、加速度の差に耐え切れなくなった身体は、途中で引きちぎられてしまう。
これを何度も繰り返し、見るも無残な状態となるが、引力の洗礼はさらに続き、分子、原子レベルまで分裂し、最終的には素粒子へと帰す。それらはブラックホールの中心に向かって進み、同書では「チューブから押し出される歯磨きペースト」のようになるという。
ペンローズ過程
さあ、あとはペンローズ過程さえわかれば、インターステラーがとっても楽しくなります。
と思ったのですが、わたしのにわか知識ではこれを簡略化して説明出来そうにありません。
かなりざっくりといきます。
まず、ペンローズ過程とは何か?というと結論から言えばブラックホールを利用してエネルギーを得る方法です。
そして、ペンローズ過程が使えるブラックホールは、カー・ブラックホールです。
カー・ブラックホールには、エルゴ球というものが存在します。

カーブラックホール(シュタインズゲートまとめより)
エルゴ球(エルゴきゅう、ergosphere)とは回転するブラックホールの外に位置する領域である。
その名前はギリシア語の仕事を意味するergonの語から来ている。
エネルギーと質量をブラックホールのこの領域から取り出すことが理論的に可能なことから、ジョン・ホイーラーらによってこの名前が付けられた。
Wikipediaより引用
カー・ブラックホールをうまく使えばエネルギーを得る方法が出来るということなのです。
具体的な方法としては、宇宙船でエルゴ球と事象の地平面の間に行き、そこで不要なものを捨てます。
そうすると、その捨てた物体の質量+αのエネルギーを得られるというわけです。
なんのこっちゃかも知れませんが、これは計算で算出されていて理論上は可能ということです。
要するに捨てた分だけエネルギーが得られる、ということです。
もう少し詳しく説明してみます。
エルゴ球と事象の地平面の間では、あらゆる物体は静止出来ないということになっています。
なんのエネルギーも無しに、動き続けられる空間(強制的に)ということです。
そこで、ゴミなどの不要なものを捨てるとします。
物体は動き続けていますので、単純に加速することになります。
つまり、ブラックホールからエネルギーを取り出しているということになります。
ブラックホールのエネルギーを取り出しているわけですから、これをずっと続けると、ブラックホールも消滅します。
すさまじくざっくりですが、こんな感じです。
さらに詳しく知りたい場合はwikipediaをどうぞ。
Wikipedia-ペンローズ過程
http://ja.wikipedia.org/wiki/ペンローズ過程
これ以上下に行くと完全にネタバレです。
私の感想を書きたいままに書いてます。
ネタバレ感想
ここからはネタバレなので、悪いことは言いませんからまだ見てない方はまず映画を見たほうがいいと思います。
みてから、あーだこーだ一緒に考えようではありませんか。
とりあえず、もう一度オフィシャルサイト貼っておきます。
インターステラー公式サイト/
予告編を見ると、ストーリー的には地球滅亡と家族愛を絡めたストーリですし、私も宇宙ものだからとりあえず見に行くか、という感じだったのですが、とんでもなかったです。
ストーリーはもちろんよく出来ていますし、家族愛を絡めたストーリーはSFに全く興味の無い人でも楽しめるようです(妻談)
でもSF好きにとっては、家族が最後にどうなろうとどうでもいいわ!という感じのストーリー展開です。
(どうでもいいわ!はちょっと大げさですが、そのくらい度肝を抜かれたのです。)
まず何がスゴイって映像です。特にブラックホールの描写。
そもそもこの映画、本物の物理学者が監修に加わっています。
キップ・ソーン博士ですね。
スティーヴン・ホーキングらとの学問上の賭けのエピソードが知られ「裸の特異点は存在するか」という賭けでホーキングに勝ち、ペントハウス1年分を受け取ったことをナショナルジオグラフィックチャンネルで語っている。「ブラックホールに落ちた物質が保持していた情報は永久に失われるか」という賭けでは失われるほうに賭けたソーンとホーキングはジョン・プレスキルに敗れて百科事典を送った。
あのホーキング博士と論を交わすほどのガチの物理学者です。
その物理学者が、映像でブラックホールを表現しているのですからそりゃまあスゴイです。
メイキング映像があるので貼っておきます。
キップ・ソーン博士自身も、この映像を作ってみてわかったことがたくさんあるから論文にすると言ってます。
つまり、これまで本当に誰も見たことのないブラックホール像が、この映画によって描き出されたと言っても過言ではないのです。
しかも最前線の研究結果が反映されているわけで、本物に近いブラックホールと言ってもいいと思います。
最後の最後で超スッキリ&痺れる展開
最初は、さすがに3時間って長すぎないか?と思っていたのですが、気づいたら映画終わってた、という状態です本当に。
もちろん映像もさることながら、時間を絡めたSF的展開のストーリーがこの上無く面白い。
インセプションが好きだ、という方はインセプションと同じような感覚で楽しめると思います。
最後の場面、あの本棚の裏に空間がつながった時はもう痺れました、「コレはスゴイ!」と。
最後の最後でそうくるか、と。
だってブラックホールに吸い込まれて終わり、と思うじゃないですか。
最後にクーパーが吸い込まれて、アメリアが新しい星でも探して終わり、と思いましたよ私は。
人類は滅亡したけど、新しい星でコロニーを作って人類は生き抜いたよ、的な。
でも全然違いました。
まさか、最後に全ての伏線を回収するとは。
何とも言われぬスッキリ感がありましたね。
そもそもこの映画、冒頭からわけのわからないことばかりなのです。
地球が置かれている環境もよくわからない。
テクノロジーが進歩しているのはわかるけど、どの程度なのか。
謎の現象を主人公の娘のマーフが受け取るけど、それがなんなのか?何が原因なのか?さっぱりわからない。
途中で人工知能ロボットとかも出てきますがが、これが何なのかよくわからない。
わかることといえば、地球が滅亡しそうだから救わないといけない。
救うためにNASAが地下組織化していて、人類を救う方法を研究している。
そしてクーパーは凄腕の宇宙飛行士だった、ということくらい。
ということで最後の最後まで謎は謎のままなのですが、最後で全部解決。
地球が滅亡しそうな原因とかはちょっと謎のままですが、一番気になるマーフが受け取るメッセージが解決します。
このメッセージが物語の上でものすごく大事そうな感じで出てくるのに、一時期ほったらかしになるんですよね。
で、数十年を経て、やっぱりあのメッセージには何か意味があるんだ!とマーフが気づくんです。
気づいたのはいいけど、結局そのメッセージの発信者は誰なのよ、と思うのですがこれが最後の最後で解決する。
いやー、スッキリ感。そして痺れます。
あとは音も良かった。
宇宙空間では音は出ない、ちゃんと忠実に描いてます。
それでも、ああも静と動を描き分けられるのか、と。
再ドッキングの時は、思わず手に汗握りました。
バック・トゥ・ザ・フューチャー+シックスセンス+インセプション+ゼログラビティ
シックスセンスのエッセンスとインセプションの構成、そしてゼログラビティを超える映像、という本当にスゴイ映画です。
2001年宇宙の旅を見た時の感動、と言ったら大げさかも知れないですが、そのくらいスゴイと思いました。
そしてタイムトラベルものとしては、バック・トゥ・ザ・フューチャーの系列でしょうか。
バック・トゥ・ザ・フューチャーとはテイストは全く違います。
タイムトラベルもの、という共通項のみです。
時系列が繋がる、という面白みは通ずるものがあるかなと思います。
だから、どれかの映画が好きであればきっと楽しめると思います。
本当にあっという間に3時間過ぎてしまいまして、周囲にもオススメしております。
映画も見てないけど、ここまで見てしまった方はぜひ見に行って下さい。
めちゃくちゃオススメです。
見たけど、よくわからなかったという方には時系列があります。
映画見てない方はコレ見ると、面白みが減るので見ないことをおすすめします。
どちらも映画全体の時系列です。言ってることは同じ。
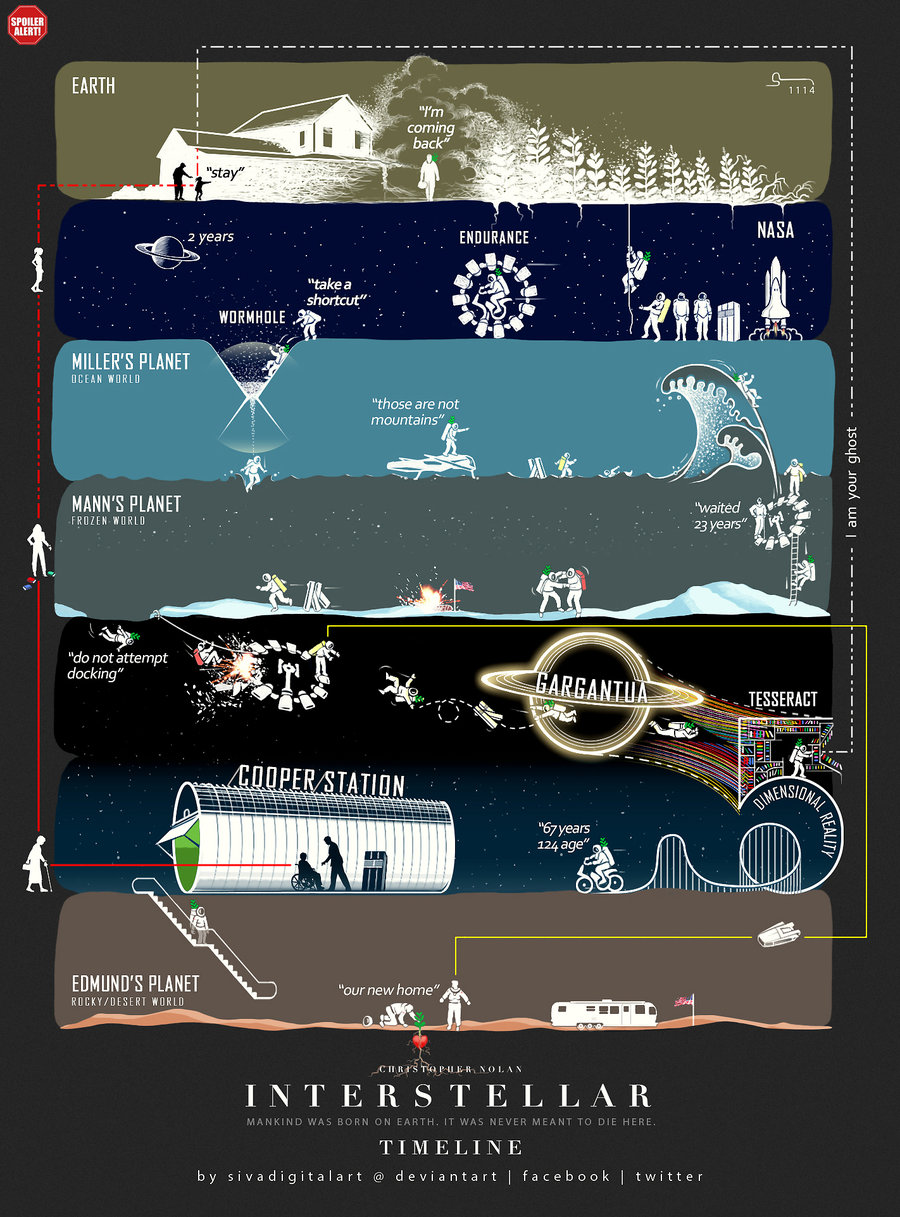
インターステラー時系列その1
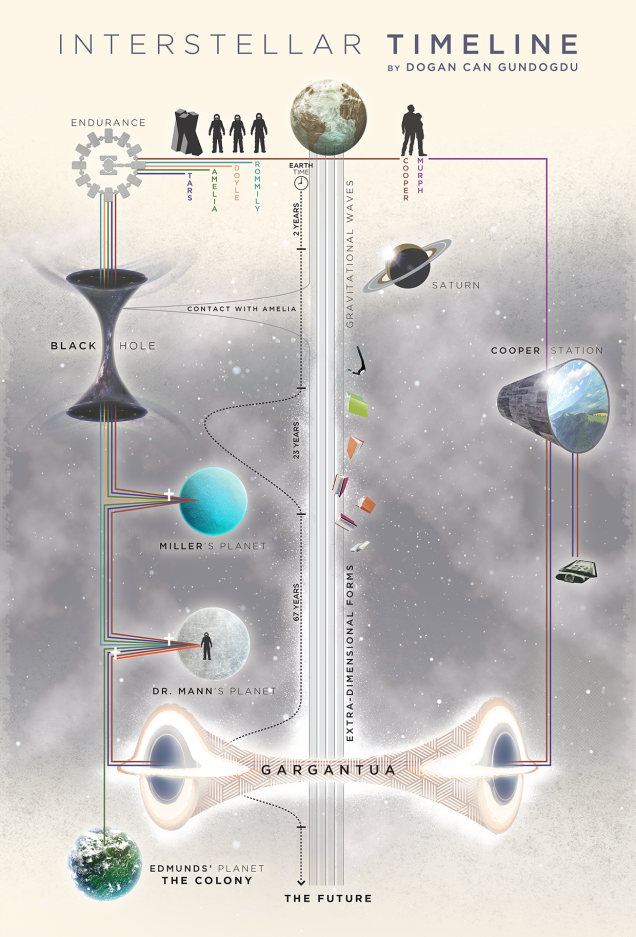
インターステラー時系列その2
コレ見てるともう一回見たくなるんですけどね。
まあ、見に行くんですけどね。